#算法

!!! note"" - 仍在探索

Basis of algorithm¶

约 1169 个字 687 行代码 2 张图片预计阅读时间 14 分钟

时间复杂度 ¶

数据结构——时间复杂度计算

排序 ¶

快排 ¶

C++

void quick_sort(int q[], int l, int r)
{
    if(l >= r) return;
    int i = l - 1, j = r + 1, x = q[(l + r) >> 1];
    while(i < j)
    {
        do i++ ;while(q[i] < x);
        do j-- ;while(q[j] > x);
        if(i < j)
        {
            int t = q[i];
            q[i] = q[j];
            q[j] = t;
        }

    }
    quick_sort(q, l, j);
    quick_sort(q, j + 1, r);

}

除了 if(l >= r) 剩下的都是 > 或者 <
do while
快速排序算法的证明与边界分析

归并 ¶

C++

void merge_sort(int q[], int l, int r)
{
    //递归的终止情况
    if(l >= r) return;

    //第一步：分成子问题
    int mid = l + r >> 1;

    //第二步：递归处理子问题
    merge_sort(q, l, mid ), merge_sort(q, mid + 1, r);

    //第三步：合并子问题
    int k = 0, i = l, j = mid + 1, tmp[r - l + 1];
    while(i <= mid && j <= r)
        if(q[i] <= q[j]) tmp[k++] = q[i++];
        else tmp[k++] = q[j++];
    while(i <= mid) tmp[k++] = q[i++];
    while(j <= r) tmp[k++] = q[j++];

    for(k = 0, i = l; i <= r; k++, i++) q[i] = tmp[k];
}

归并排序的证明与边界分析

二分 ¶

C++

//查找左边界 SearchLeft 简写SL
int SL(int l, int r)
{
    while (l < r)
    {
        int mid = l + r >> 1;
        if (check(mid)) r = mid; 
        else l = mid + 1; 
    }   
    return l;
}
//查找右边界 SearchRight 简写SR 
int SR(int l, int r) 
{
    while (l < r)
    {                   
        int mid = l + r + 1 >> 1; //需要+1 防止死循环
        if (check(mid)) l = mid;
        else r = mid - 1; 
    }
    return r; 
}

发明男左女右的真是个天才，如果包含 x 的条件是左边，就 + 1，否则不加。
二分模板

高精度 ¶

加法 ¶

C++

#include <iostream>
#include <vector>
using namespace std;
vector<int> add(vector<int> &a, vector<int> &b)
{
    vector<int> res;
    int t = 0;
    for(int i = 0; i < a.size() || i < b.size() || t;i++)
    {
        if(i < a.size()) t += a[i];
        if(i < b.size()) t += b[i];
        res.push_back(t % 10);
        t /= 10;
    }
    return res;
}
int main()
{
    string a,b;
    cin >> a >> b;
    vector<int> A,B;
    for(int i = a.size() - 1; i >= 0; i --) A.push_back(a[i] - '0');
    for(int i = b.size() - 1; i >= 0; i --) B.push_back(b[i] - '0');

    auto C = add(A,B);
    for(int i = C.size() - 1;i >= 0; i --) printf("%d",C[i]);
    return 0;
}

减法 ¶

C++

#include<iostream>
#include<vector>
using namespace std;

bool cmp(vector<int> &a, vector<int> &b)
{
    if(a.size() != b.size()) return a.size() > b.size();
    else
    {
        for(int i = a.size() - 1; i>= 0;i--)
        {
            if(a[i] != b[i]) return a[i] > b[i];
        }
        return true;
    }
}

vector<int> sub(vector<int> &a,vector<int> &b)
{
    vector<int> res;
    for(int i = 0,t = 0; i < a.size(); i++)
    {
        t = a[i] - t;
        if(i < b.size()) t -= b[i];
        res.push_back((t + 10) % 10);
        if(t < 0) t = 1;
        else t = 0;
    }
    while(res.size() > 1 && res.back() == 0) res.pop_back();
    return res;
}
int main()
{
    string a,b;
    vector<int> A,B,C;
    cin >> a >> b;
    for(int i = a.size() - 1; i >= 0; i --) A.push_back(a[i] - '0');
    for(int i = b.size() - 1; i >= 0; i --) B.push_back(b[i] - '0');

    if(cmp(A, B))
    {
        C = sub(A, B);
        for(int i = C.size() - 1; i >= 0; i--) printf("%d",C[i]);
    }
    else 
    {
        C = sub(B, A);
        printf("-");
        for(int i = C.size() - 1; i >= 0; i--) printf("%d",C[i]);
    }

    return 0;
}

乘法 ¶

C++

#include <iostream>
#include <vector>
using namespace std;

vector<int> mul(vector<int> &a, vector<int> &b)
{
    vector<int> res(a.size() + b.size(), 0);
    for(int i = 0; i < a.size(); i++)
    {
        for(int j = 0; j < b.size(); j++)
        {
            res[i + j] += a[i] * b[j];  
        }
    }
    for(int i = 0; i + 1 < res.size(); i ++)
    {
        res[i + 1] += res[i] / 10;
        res[i] = res[i] % 10;
    }
    while(!res.back() && res.size() > 1) res.pop_back(); 
    return res;
}
int main()
{
    string a,b;
    vector<int> A, B, C;
    cin >> a >> b;
    for(int i = a.size() - 1; i >= 0; i--) A.push_back(a[i] - '0');
    for(int i = b.size() - 1; i >= 0; i--) B.push_back(b[i] - '0');
    C = mul(A, B);
    for(int i = C.size() - 1; i >= 0;i--) printf("%d",C[i]);
    return 0;
}

高精度乘法分析

除法 ¶

C++

#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;

vector<int> div(vector<int> &a, int b, int &r)
{
    vector<int> res;
    int t = 0;
    for(int i = a.size() - 1; i >= 0; i--)
    {
        t = t * 10 + a[i];
        res.push_back(t / b);
        t %= b;
    }
    r = t;
    reverse(res.begin(), res.end());
    while(res.size() > 1 && !res.back()) res.pop_back();
    return res;
}
int main()
{
    string a;
    int b, r;
    vector<int> A, C;
    cin >> a >> b;
    for(int i = a.size() - 1; i >= 0; i--) A.push_back(a[i] - '0');
    C = div(A, b, r);
    for(int i = C.size() - 1; i >= 0; i--) printf("%d",C[i]);
    cout << endl;
    cout << r << endl;

    return 0;
}

前缀 & 差分 ¶

首先给定一个原数组 a： a[1], a[2], a[3],,,,,, a[n];
然后我们构造一个数组b ： b[1] ,b[2] , b[3],,,,,, b[i];
使得 a[i] = b[1] + b[2]+ b[3] +,,,,,, + b[i]
也就是说，a数组是b数组的前缀和数组，反过来我们把 b 数组叫做 a 数组的差分数组。换句话说，每一个 a[i] 都是 b 数组中从头开始的一段区间和。

前缀 ¶

一维：

C++

#include <iostream>

using namespace std;
const int N = 100010;
int n, m;
int a[N], s[N];
int main()
{
    cin >> n >> m;
    for(int i = 1; i <= n; i++) scanf("%d",&a[i]);
    for(int i = 1; i <= n; i++) s[i] = s[i - 1] + a[i];
    while(m --)
    {
        int a, b;
        scanf("%d%d",&a, &b);
        printf("%d\n", s[b] - s[a - 1]);
    }

    return 0;
}

二维：

C++

#include <iostream>
using namespace std;

const int N = 1001;
int n, m, q;
int a[N][N],s[N][N];

int main()
{
    scanf("%d%d%d",&n,&m,&q);
    for(int i = 1; i <= n; i++)
    {
        for(int j = 1; j <= m; j ++)
        {
            scanf("%d", &a[i][j]);
        }
    }
    for(int i = 1;i <= n; i++)
    {
        for(int j = 1; j <= m; j++)
        {
            s[i][j] = s[i - 1][j] + s[i][j - 1] - s[i - 1][j - 1] + a[i][j]; 
        }
    }
    while(q--)
    {
        int x1,y1,x2,y2;
        scanf("%d%d%d%d", &x1, &y1, &x2, &y2);
        printf("%d\n",s[x2][y2] - s[x2][y1 - 1] - s[x1 - 1][y2] + s[x1 - 1][y1 - 1]);
    }
    return 0;
}

差分 ¶

一维：

C++

#include <iostream>
using namespace std;

const int N = 100010;
int n, m;
int a[N], b[N];

int main()
{
    scanf("%d%d",&n, &m);
    for(int i = 1;i <= n; i++) scanf("%d", &a[i]);
    for(int i = 1;i <= n; i++) b[i] = a[i] - a[i - 1];
    while(m --)
    {
        int l, r, c;
        scanf("%d%d%d", &l, &r, &c);
        b[l] += c;
        b[r + 1] -= c;

    }
     for(int i = 1; i <= n; i++) a[i] = a[i - 1] + b[i];
     for(int i = 1; i <= n; i++) printf("%d ", a[i]);

    return 0;
}

二维：

C++

#include<iostream>
#include<cstdio>
using namespace std;
const int N = 1e3 + 10;
int a[N][N], b[N][N];
void insert(int x1, int y1, int x2, int y2, int c)
{
    b[x1][y1] += c;
    b[x2 + 1][y1] -= c;
    b[x1][y2 + 1] -= c;
    b[x2 + 1][y2 + 1] += c;
}
int main()
{
    int n, m, q;
    cin >> n >> m >> q;
    for (int i = 1; i <= n; i++)
        for (int j = 1; j <= m; j++)
            cin >> a[i][j];
    for (int i = 1; i <= n; i++)
    {
        for (int j = 1; j <= m; j++)
        {
            insert(i, j, i, j, a[i][j]);      //构建差分数组
        }
    }
    while (q--)
    {
        int x1, y1, x2, y2, c;
        cin >> x1 >> y1 >> x2 >> y2 >> c;
        insert(x1, y1, x2, y2, c);
    }
    for (int i = 1; i <= n; i++)
    {
        for (int j = 1; j <= m; j++)
        {
            b[i][j] += b[i - 1][j] + b[i][j - 1] - b[i - 1][j - 1];  //二维前缀和
        }
    }
    for (int i = 1; i <= n; i++)
    {
        for (int j = 1; j <= m; j++)
        {
            printf("%d ", b[i][j]);
        }
        printf("\n");
    }
    return 0;
}

分析

双指针 ¶

C++

#include <iostream>
using namespace std;

const int N = 100010;
int n;
int a[N], s[N];
int main()
{
    int res = 0;
    cin >> n;
    for(int i = 0; i < n; i++) scanf("%d",&a[i]);
    for(int i = 0, j = 0; i < n; i++)
    {
        s[a[i]] ++; // s[] 记录的是 i, j 双指针维护区间中 某个数出现的次数
        while(s[a[i]] > 1)
        {
            s[a[j]]--;
            j++;
        }
        res = max(res, i - j + 1);
    }
    cout << res << endl;

    return 0;
}

位运算 ¶

运算符	描述	运算规则	示例（`a = 5`, `b = 3`）	结果
`&`	按位与（AND）	只有两个对应位都为 1，结果才为 1	`5 & 3` → `0101 & 0011`	`1`
`\|`	按位或（OR）	只要两个对应位中有一个为 1，结果为 1	`7`
`^`	按位异或（XOR）	两个位不同则为 1，相同则为 0	`5 ^ 3` → `0101 ^ 0011`	`6`
`~`	按位非（NOT）	将所有位取反	`~5` → `~0101`	`-6`
`<<`	左移（Left Shift）	将位向左移动，右侧补 0	`5 << 1` → `0101 << 1`	`10`
`>>`	右移（Right Shift）	将位向右移动，左侧补 0 或符号位	`5 >> 1` → `0101 >> 1`	`2`
`&=`	按位与赋值（AND Assignment）	`a = a & b`	`a &= b`	`a` 更新为 `a & b`
`\| =`	按位或赋值（OR Assignment）	`a = a \| b`
`^=`	按位异或赋值（XOR Assignment）	`a = a ^ b`	`a ^= b`	`a` 更新为 `a ^ b`
\|	按位或	有一个为 1 结果就为 1

检查奇偶性：

使用按位与运算检查一个数是否为奇数或偶数。
n & 1 == 0 表示 n 是偶数，n & 1 == 1 表示 n 是奇数

交换两个数（不使用临时变量）：

使用异或运算可以交换两个数的值。

C++

int a = 5, b = 3;
a = a ^ b;  // a = 5 ^ 3 = 6
b = a ^ b;  // b = 6 ^ 3 = 5
a = a ^ b;  // a = 6 ^ 5 = 3

设置、清除和取反特定位：

设置某一位为 1：
x |= (1 << k); 将 x 的第 k 位设置为 1。
清除某一位为 0：
x &= ~(1 << k); 将 x 的第 k 位设置为 0。
取某一位的值：
(x >> k) & 1; 取出 x 的第 k 位

判断某一位是否为 1：

可以通过 (n >> k) & 1 来判断 n 的第 k 位是否为 1。如果结果为 1，表示该位为 1，否则为 0

清除最低位的 1：

n & (n - 1) 可以清除一个数的最低位的 1。例如，如果 n = 12（二进制是 1100），则 n - 1 = 11（二进制是 1011），n & (n - 1) = 1000，即 8，去掉了最低位的 1

计算整数的二进制位数：

可以通过不断右移来计算一个整数的二进制位数。例如，int bit_count = 0; while (n > 0) { n >>= 1; bit_count++; }

判断一个数是否为 2 的幂：

任何 2 的幂数，二进制表示中只有一个 1。可以使用 n & (n - 1) 判断一个数是否为 2 的幂：如果结果是 0，那么 n 是 2 的幂。

C++

bool isPowerOfTwo(int n) {
    return (n > 0) && ((n & (n - 1)) == 0);
}

离散化 ¶

C++

#include <iostream>
#include <vector>
#include <algorithm>

using namespace std;

int n, m;
const int N = 300010;
vector<int> alls;
vector<pair<int, int>> add, quiry;
int a[N],s[N];

int find(int x)
{
    int l = 0, r = alls.size() - 1;
    while(l < r)
    {
        int mid = l + r >> 1;
        if(alls[mid] >= x) r = mid;
        else l = mid + 1;
    }
    return r + 1; // 离散化坐标的下标从 1 开始
}
int main()
{
    scanf("%d%d",&n, &m);
    for(int i = 1; i <= n; i++)
    {
        int x, c;
        scanf("%d%d",&x, &c);
        add.push_back({x, c});
        alls.push_back(x);
    }

    for(int i = 1; i <= m; i++)
    {
        int l, r;
        scanf("%d%d",&l,&r);
        alls.push_back(l);
        alls.push_back(r);
        quiry.push_back({l, r}); // 到这里所有数据存好了
    }
    sort(alls.begin(), alls.end()); //排序
    alls.erase(unique(alls.begin(), alls.end()), alls.end()); //去重

    for(auto item : add)
    {
        int x = find(item.first);
        a[x] += item.second;      // 对应的坐标增加输入值
    }
    for(int i = 1; i <= alls.size(); i++) s[i] = s[i - 1] + a[i]; //求前缀和
    for(auto item : quiry)
    {
        int l = find(item.first);
        int r = find(item.second);
        printf("%d\n", s[r] - s[l - 1]);

    }

    return 0;
}

将查找区间压缩，提高搜索效率

区间合并 ¶

C++

#include <iostream>
#include <algorithm>
#include <vector>
using namespace std;

const int N = 100010;
int n;
typedef pair<int, int> pII;
vector<pII> segs,res;

int main()
{
    cin >> n;
    while(n --)
    {
        int l,r;
        scanf("%d%d",&l, &r);
        segs.push_back({l, r});
    }
    sort(segs.begin(), segs.end()); // 按左端点排序
    int st = -2e9, ed = -2e9;
    for(auto item : segs)
    {
        if(ed < item.first) // 
        {
            if(ed != -2e9) res.push_back({st, ed}); // 如果交错就存入上一个维护的区间，并且避免了第一个无效区间的情况。
            st = item.first, ed = item.second; // 维护下一个区间
        }
        else
        {
            ed = max(ed, item.second); // 确定合并后的ed
        }
    }
    res.push_back({st, ed}); // 放入维护的最后一个区间
    cout << res.size();

    return 0;
}

链表 ¶

哈希表 ¶

哈希表可以通过 key 在 O(1) 时间复杂度找到这个 key 对应的 value
key 值唯一，value 可以重复

哈希表伪码逻辑

C++

class MyHashMap {

private:
    vector<void*> table;

public:
    // 增/改，复杂度 O(1)
    void put(auto key, auto value) {
        int index = hash(key);
        table[index] = value;
    }

    // 查，复杂度 O(1)
    auto get(auto key) {
        int index = hash(key);
        return table[index];
    }

    // 删，复杂度 O(1)
    void remove(auto key) {
        int index = hash(key);
        table[index] = nullptr;
    }

private:
    // 哈希函数，把 key 转化成 table 中的合法索引
    // 时间复杂度必须是 O(1)，才能保证上述方法的复杂度都是 O(1)
    int hash(auto key) {
        // ...
    }
};

拉链法解决哈希冲突

C++

class ExampleChainingHashMap {

    // 链表节点，存储 key-value 对儿
    // 注意这里必须存储同时存储 key 和 value
    // 因为要通过 key 找到对应的 value
    struct KVNode {
        int key;
        int value;

        // 为了简化，我这里直接用标准库的 LinkedList 链表
        // 所以这里就不添加 next 指针了
        // 你当然可以给 KVNode 添加 next 指针，自己实现链表操作
        KVNode(int key, int value) : key(key), value(value) {}
    };

    // 底层 table 数组中的每个元素是一个链表
    std::vector<std::list\<KVNode>> table;

public:
    ExampleChainingHashMap(int capacity) : table(capacity) {}

    int hash(int key) {
        return key % table.size();
    }

    // 查
    int get(int key) {
        int index = hash(key);

        if (table[index].empty()) {
            // 链表为空，说明 key 不存在
            return -1;
        }

        for (const auto& node : table[index]) {
            if (node.key == key) {
                return node.value;
            }
        }

        // 链表中没有目标 key
        return -1;
    }

    // 增/改
    void put(int key, int value) {
        int index = hash(key);

        if (table[index].empty()) {
            // 链表为空，新建一个链表，插入 key-value
            table[index].push_back(KVNode(key, value));
            return;
        }

        // 链表不为空，要遍历一遍看看 key 是否已经存在
        // 如果存在，更新 value
        // 如果不存在，插入新节点
        for (auto& node : table[index]) {
            if (node.key == key) {
                // key 已经存在，更新 value
                node.value = value;
                return;
            }
        }

        // 链表中没有目标 key，添加新节点
        // 这里使用 push_back 添加到链表尾部
        // 因为 c++ std::list 的底层实现是双链表，头尾操作都是 O(1) 的
        // https://labuladong.online/algo/data-structure-basic/linkedlist-implement/
        table[index].push_back(KVNode(key, value));
    }

    // 删
    void remove(int key) {
        auto& list = table[hash(key)];
        if (list.empty()) {
            return;
        }

        // 如果 key 存在，则删除
        // 这个 remove_if 方法是 c++ std::list 的方法，可以删除满足条件的元素，时间复杂度 O(N)
        list.remove_if([key](KVNode& node) { return node.key == key; });
    }
};

面试模拟

1、为什么我们常说，哈希表的增删查改效率都是 O(1) ？

因为哈希表底层就是操作一个数组，其主要的时间复杂度来自于哈希函数计算索引和哈希冲突。只要保证哈希函数的复杂度在 O(1)O(1)，且合理解决哈希冲突的问题，那么增删查改的复杂度就都是 O(1)O(1)。

2、哈希表的遍历顺序为什么会变化？

因为哈希表在达到负载因子时会扩容，这个扩容过程会导致哈希表底层的数组容量变化，哈希函数计算出来的索引也会变化，所以哈希表的遍历顺序也会变化。

3、哈希表的增删查改效率一定是 O(1) 吗？

不一定，正如前面分析的，只有哈希函数的复杂度是 O(1)，且合理解决哈希冲突的问题，才能保证增删查改的复杂度是 O(1)。

哈希冲突好解决，都是有标准答案的。关键是哈希函数的计算复杂度。如果使用了错误的 key 类型，比如前面用 ArrayList 作为 key 的例子，那么哈希表的复杂度就会退化成 O(N)。

4、为啥一定要用不可变类型作为哈希表的 key？

因为哈希表的主要操作都依赖于哈希函数计算出来的索引，如果 key 的哈希值会变化，会导致键值对意外丢失，产生严重的 bug。

二叉树 ¶

满二叉树
完全二叉树：完全二叉树是指，二叉树的每一层的节点都紧凑靠左排列，且除了最后一层，其他每层都必须是满的
平衡二叉树： 每个节点的左子树和右子树的高度差不超过 1

Text Only

# 这是一棵平衡二叉树
    1
   / \
  2   3
 /   / \
4   5   6
     \
      7

# 这不是，因为 2 节点的左右子树高度差为 2
    1
   / \
  2   3
 /   / \
4   5   6
 \   \
  8   7

二叉搜索树 (BST)： 每个节点的左子树上的所有节点的值都要小于此节点的值，每个节点的右子树上的所有节点的值都要大于此节点的值。

Text Only

# BST
    7
   / \
  4   9
 / \   \
1   5   10

# not a BST
    7
   / \
  4   9
 / \   \
1   8   10

二叉树的实现

C++

class TreeNode {
public:
    int val;
    TreeNode* left;
    TreeNode* right;
    TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
};

// 你可以这样构建一棵二叉树：
TreeNode* root = new TreeNode(1);
root->left = new TreeNode(2);
root->right = new TreeNode(3);
root->left->left = new TreeNode(4);
root->right->left = new TreeNode(5);
root->right->right = new TreeNode(6);

// 构建出来的二叉树是这样的：
//     1
//    / \
//   2   3
//  /   / \
// 4   5   6

递归遍历 (DFS): 常用于找所有路径

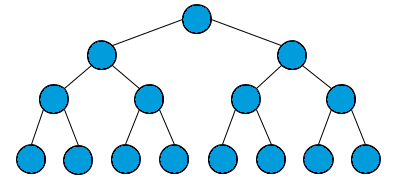
DFS

C++

class TreeNode {
public:
    int val;
    TreeNode* left;
    TreeNode* right;

    TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
};

// 二叉树的遍历框架
void traverse(TreeNode* root) {
    if (root == nullptr) {
        return;
    }
    traverse(root->left);
    traverse(root->right);
}

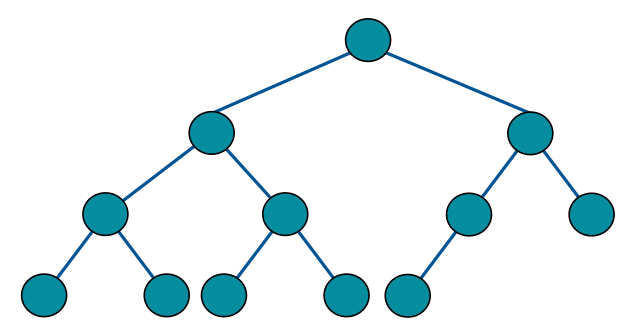
层序遍历 (BFS)：常用于找最短路径

BFS-1

C++

void levelOrderTraverse(TreeNode* root) {
    if (root == nullptr) {
        return;
    }
    std::queue<TreeNode*> q;
    q.push(root);
    while (!q.empty()) {
        TreeNode* cur = q.front();
        q.pop();
        // 访问 cur 节点
        std::cout << cur->val << std::endl;

        // 把 cur 的左右子节点加入队列
        if (cur->left != nullptr) {
            q.push(cur->left);
        }
        if (cur->right != nullptr) {
            q.push(cur->right);
        }
    }
}

BFS-2

C++

void levelOrderTraverse(TreeNode* root) {
    if (root == nullptr) {
        return;
    }
    queue<TreeNode*> q;
    q.push(root);
    // 记录当前遍历到的层数（根节点视为第 1 层）
    int depth = 1;

    while (!q.empty()) {
        int sz = q.size();
        for (int i = 0; i < sz; i++) {
            TreeNode* cur = q.front();
            q.pop();
            // 访问 cur 节点，同时知道它所在的层数
            cout << "depth = " << depth << ", val = " << cur->val << endl;

            // 把 cur 的左右子节点加入队列
            if (cur->left != nullptr) {
                q.push(cur->left);
            }
            if (cur->right != nullptr) {
                q.push(cur->right);
            }
        }
        depth++;
    }
}

多叉树 ¶

DFS

C++

void traverse(Node* root) {
    if (root == nullptr) {
        return;
    }
    // 前序位置
    for (Node* child : root->children) {
        traverse(child);
    }
    // 后序位置
}

C++

Reference¶

https://labuladong.online/algo/home/