跳转至
#course_notes

CS61C 课程笔记

约 596 个字 31 行代码 7 张图片 预计阅读时间 3 分钟

  • @start 2025.3.23
  • @end...
  • 先上传，强迫学习，写完整理

image.png

Stack（栈）:

  • 存储局部变量、函数参数、返回地址
  • 自动分配和释放
  • 从高地址向低地址增长
  • 大小有限，可能栈溢出

Heap（堆）:

  • 动态分配的内存（malloc/free）
  • 从低地址向高地址增长
  • 需要手动管理内存
  • 可能发生内存泄漏或碎片化

Static Data（静态数据）:

  • 全局变量
  • 静态变量
  • 常量数据
  • 程序运行期间一直存在

Code（代码段）:

  • 程序的机器指令
  • 只读
  • 程序加载时确定
C
void* malloc(size_t size);
int *p = (int *)malloc(sizeof(int) * 5);  // 分配5个int的空间
// - 分配指定字节数的内存
// - 内存内容是未初始化的（随机值）
// - 返回void*指针，需要类型转换
// - 失败返回NULL
void* calloc(size_t num, size_t size);
int *p = (int *)calloc(5, sizeof(int));  // 分配5个int的空间
// - 分配 num*size 字节的内存
// - 自动将内存初始化为0
// - 返回void*指针
// - 失败返回NULL
void free(void* ptr);
free(p);  // 释放之前分配的内存
// - 释放之前malloc/calloc分配的内存
// - 不会把指针设为NULL
// - 释放后继续使用是未定义行为
void* realloc(void* ptr, size_t new_size);
p = (int *)realloc(p, sizeof(int) * 10);  // 扩展到10个int
// - 调整已分配内存的大小
// - 可能会移动到新位置
// - 新增部分未初始化
// - 失败返回NULL但不改变原内存

一些心得： - 每个 malloc/calloc 都要配对 free - free 后设置指针为 NULL 避免悬挂指针 - 总是检查 malloc/calloc/realloc 的返回值 - realloc (NULL, size) 等价于 malloc (size) - realloc (ptr, 0) 等价于 free (ptr)

关于 unions

C
union fubar {
    int a;      // 4字节
    char *b;    // 8字节（64位系统）
    void **c;   // 8字节（64位系统）
} Fubar;
- 所有成员共享一块内存 - 内存大小等于最大成员大小 - 同一时间只能安全使用一个成员
C
Fubar *f = (Fubar *)malloc(sizeof(union fubar));
f->a = 1312;    // 现在这块内存被当作int使用
f->b = "baz";   // 现在同一块内存被当作char*使用

关于 struct 的内存对齐，我在 [[C 语言 #3.2 结构体内存对齐 ]] 中有提及

关于 GC (conservative garbage) 保守式 GC 的问题 - 不能移动内存，导致内存碎片化 - 需要停止程序运行（Stop the World）来进行垃圾回收 - 导致程序暂停，影响性能 python 的解决方案 - 引用计数，可以随时释放，但是无法处理循环引用

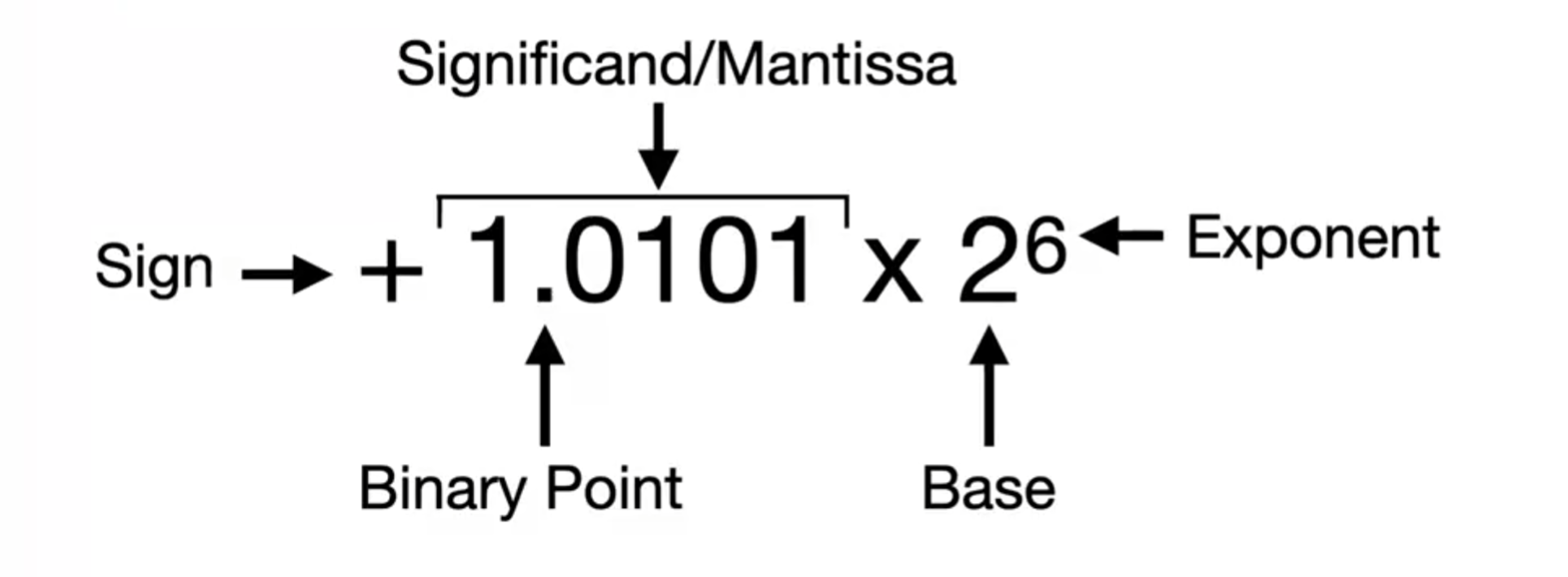
image.png

image.png

every number must have a "1" in the left (except "0"), that means we can save room for the leftmost "1"

image.png

  • bias fomual \(N=-(2^{n-1}-1)\)
  • 这个偏置可以方便地将有符号数转换为无符号数
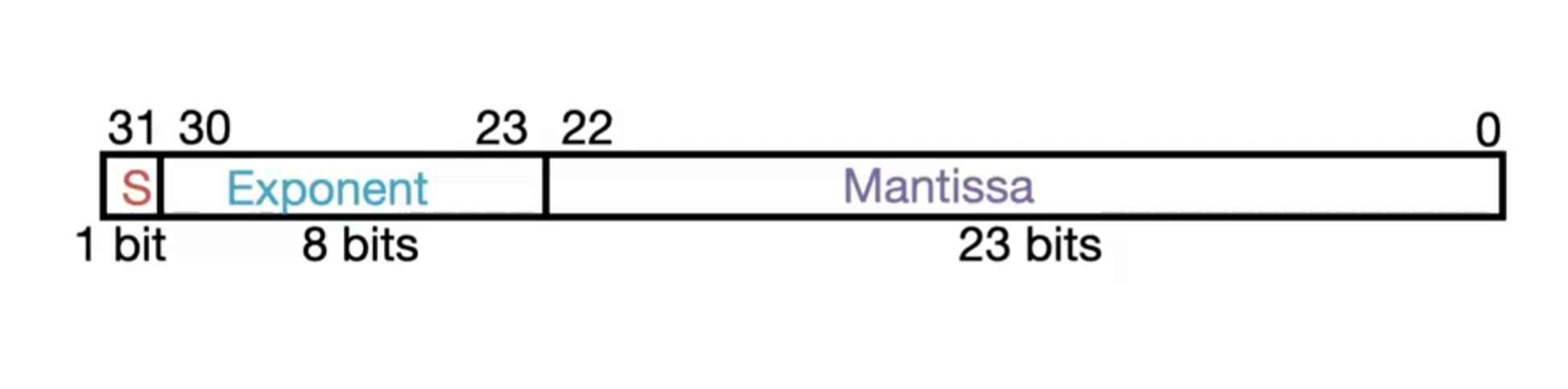
  • 浮点数可以表示为 \((-1)^{s}\times 1.mantissa\times 2^{exponent-127}\)

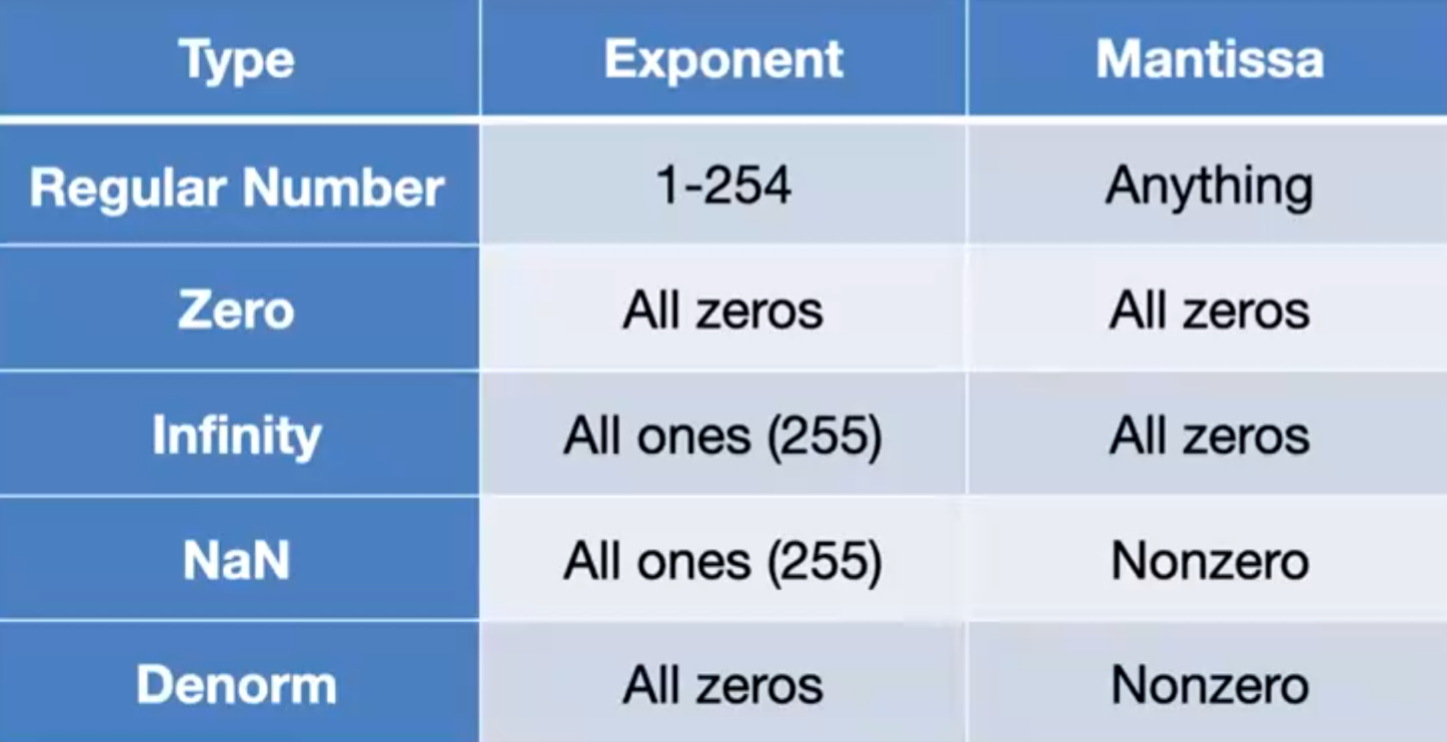
image.png

表示的最小的正数为， \(2^{-126}\) ，如果 exponent = allzeros 就是 0 了 表示的最大的正数为， 0|11111110|111111111111111111111111 = \((2-2^{-23})\times 2^{127}\) 负数的范围同理

下图中有颜色的区域不能表示 image.png

表示 norm： \((1+y)*2^{x-127}\) ，其中 y 是 mantissa，x 是 exponent 下一个数字 \((1+y+2^{-23})*2^{x-127}\) ,所以步长就是 \(2^{-23}*2^{x-127}=2^{x-150}\) ,可以看出来步长会随着指数的滚动而变化

denormalized formula: \((-1)^{s}\times 0.mantissa\times 2^{-126}\) , 为了表示更接近零的数字 denorm range: \(2^{-126}\sim2^{-149}\) 表示 denorm: \(y*2^{-126}\) ,下一个数字 \((y+2^{-23})*2^{-126}\) 步长为 \(2^{-149}\) 不变

一个例子： image.png